The collapse of rational certainty

I want to take you back—in imagination—to the time when the upper echelons of society had utter confidence in their own rightness, rooted in rationality and religious rectitude. For centuries, the systematic mode had provided certainty, based on those illusory understandings of meaningness. I want to show you their shock, horror, and bewilderment as their justifications fell through beneath them.

Unfortunately, I cannot do that, because I am incapable of imagining such certainty. Probably you are too. I have lived all my life in a culture that constantly reinforces the message that meaning is a matter of perspective. People’s opinions about politics, ethics, aesthetics are a matter of choice, or personality, or based on individual experiences, or culture, or other arbitrary factors. Even supposed scientific truths, like about covid or global warming, are essentially contested and inherently uncertain. Contemporary Westerners may have our own strong opinions, but we literally cannot imagine what it would be like to live in a world where everyone takes for granted that there are well-known, generally-agreed-upon ultimate truths of such matters.

Leaders’ total confidence in society’s correctness contributed to the extraordinary achievements of the systematic era.¹ That was shattered in the early 1900s, partly by a series of foundational crises in rationality and religion. This page explains the collapse of rationalism; I cover the disintegration of religion in the next chapter, on the countercultures.

The promise of rationalism was that everything can be known with certainty, and understood and controlled, by applying the eternally-correct methods of reasoning. This was true enough to bring about the Scientific Revolution, the Industrial Revolution, reasonably well governed democracies, great advances in health, life expectancy, living standards, human rights, and saner public morality. There was every reason to suppose progress would continue and accelerate.

Unfortunately, in the early twentieth century, rationalism delved too deep, undermined its own foundations, and awakened eldritch horrors. By the middle of the century, the inescapable conclusion was that rationality, science, and mathematics cannot supply the ultimate justifications that seemed possible in the 1800s. It is not true that everything—or even anything—can be known with certainty; nor fully understood or controlled. There is no absolutely correct method of reasoning. The promises of rationalist eternalism, which underwrote the optimism of the systematic mode, cannot be fulfilled by any means.

I believe this was a major factor in the breakdown of the systematic mode, and the several phases of disintegration of meaning through the rest of the century.² Leaders of social and cultural systems were well enough educated to understand that rationalism had failed, although probably not the details of how or why. That induced a profound loss of confidence. When challenged by the anti-rational countercultures of the 1960s–90s, they could not justify status quo institutions, and relinquished power relatively peacefully.

The foundational crises proved that rationality does not always work. Unfortunately, the word “always” gets too often forgotten. Incoherent irrationality is typical of our present, atomized mode. Institutional failures during the covid crisis, combined with popular pseudoscientific resistance to even sensible public health policies, may be a foretaste of greater catastrophes.

Rationality works much of the time—not just in science and mathematics, but in many dimensions of meaning as well: in politics, ethics, and aesthetics, for example. Restoring respect for a relativized rationality will be key to our upcoming transition to the fluid mode. It may herald a new age of progress, not just material but in dimensions of meaning as well, outshining anything the systematic mode could imagine.

The end of rationalist certainty was not a single event. It came as a series of unexpected, unwanted discoveries, throughout the first half of the twentieth century. Here I cover only some key events: non-Euclidean geometry, Einstein’s general relativity, quantum theory, and the foundational crisis in mathematics caused by problems with infinities and in logic.

The Elements of Absolute Truth

For thousands of years, every educated Westerner understood that mathematics was the direct route to the Mind of God. That may sound absurd now, when religious people often revile technical rationality, but it was true from 500 BC until about a hundred years ago.

Many Ancient Greeks had a powerful religious certainty that everything in the material world must follow mathematical laws. It’s difficult to understand why, because they had only two examples, neither of which quite worked, and virtually everything else was a counterexample. The theory of musical harmony based on integer ratios of string lengths was one near-success,³ and the Ptolemaic scheme for calculating planetary motions was the other.⁴

Fortunately, it seemed that mathematics can at least provide certainty about itself. Euclid’s Elements was the sacred source of rationality. It was the standard geometry textbook, used unchanged for two thousand years, up until about 1900. By definition, every educated European had to have read and understood the Elements.

The Elements taught the method of mathematical proof. Euclid started from ten simple, unquestionably true facts no one could argue with. From these “axioms,” he derived complex non-obvious insights. Each step in the proof was also simple and unarguable. Each compelled agreement, leading you down a path to an unexpected conclusion. Therefore, you knew everything in the Elements was absolutely certainly true.

The Elements became the standard of rationality in general, not just in mathematics. Starting from unarguable axioms concerning some topic, you perform a series of unarguably correct deductions that demonstrate whatever you wanted to prove: QED.

This was the ideal for all systems of meaning. If you wanted to justify political or moral or legal claims, for example, you tried to set them out in the form of Euclidean proofs. In the mid-1600s, Baruch Spinoza produced an ethical theory—still influential—that he modeled on Euclid’s Elements, titled Ethics Demonstrated in Geometrical Order. Two hundred years later, Abraham Lincoln, who grew up in poverty and was almost entirely self-educated, wrote:

In the course of my law reading I constantly came upon the word “demonstrate.” I thought at first that I understood its meaning, but soon became satisfied that I did not…. I consulted Webster’s Dictionary. They told of “certain proof,” “proof beyond the possibility of doubt”; but I could form no idea of what sort of proof that was…. At last I said, Lincoln, you never can make a lawyer if you do not understand what demonstrate means; and I left my situation in Springfield, went home to my father’s house, and stayed there till I could give any proposition in the six books of Euclid at sight. I then found out what demonstrate means, and went back to my law studies.

For many, mathematical certainty was also a basis for religious certainty. God was the Supreme Rationalist, who created the cosmos in accord with mathematical structures that exist eternally in His Mind, outside space and time. By examining His Creation, we can find its underlying logic. That gives us a view into the Divine Rationality, and therefore absolute certainty concerning the nature and intention of God. St. Augustine, whose synthesis of Biblical myths and Ancient Greek rationalism formed the philosophical basis for Western Christianity, wrote:

If you see anything at all that has measure, number, and order, do not hesitate to attribute it to God as craftsman. If you take away all measure, number, and order, there is absolutely nothing left.

Newton, more certain than God

Nature and Nature’s laws lay hid in night:
God said, Let Newton be! — and all was light.
—Alexander Pope, 1727

After two thousand years of all rational people knowing that mathematics must somehow explain everything, Isaac Newton finally proved that it did. Thank God!

Newton’s physics was based on Euclid’s Elements, and therefore was absolutely certain.⁵ He made extensive use of the Euclidean understanding of space, and the deductive methods of mathematical proof. Like Euclid, Newton’s physics is simple and elegant. Any reasonably bright high school student can learn the whole thing, and it all seems like common sense once you do.⁶

Mathematical physics gave, again, an unobstructed view of God: an understanding of His Will as manifest in His Creation. And, it seemed that it could explain everything. It was a complete theory of material existence. Or anyway, it should be one, and surely would be one, once the details got worked out.

Science and mathematics even became more certain than God. By 1800, many educated people doubted God, but no one could doubt Euclid’s geometry, nor Newton’s Laws of Motion. Those were absolute truths, true eternally and everywhere without exception. You didn’t need to believe anything, to take anything on faith: they were proven true by easy-to-follow logic that no one could possibly argue with.

Together with the Elements, Newton’s Laws became the prototype of systematic rationality for the European Enlightenment. If it works for gravity, why not for government, ethics, art, religion? And, to an astonishing extent, it did.

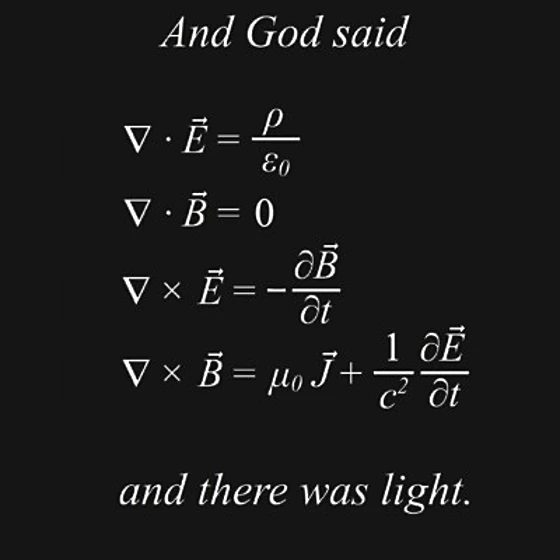
Newton didn’t fully explain light or magnetism, but that got done by the end of the 1800s. Or so it seemed! Four simple, elegant equations explained all known facts with perfect precision.⁷ As of 1900, physicists could confidently declare: “There is nothing new to be discovered in physics now. All that remains is more and more precise measurement.”⁸

With physics completed, explaining everything else seemed imminent. This was the fantasy of reductionism, that all knowledge should be applications of physics.

When parallel lines go bad

One of Euclid’s axioms was somewhat more complicated than the others, and less obviously true. It can be stated as: Given a line, and a point not on the line, you can draw only one other line that goes through the point and doesn’t intersect the original line. The new line will be parallel to the original one, so this is called the parallel postulate.⁹

The postulate is pretty obviously true, but why? For more than two thousand years, mathematicians tried to prove it true—and failed.

In the early 1800s, several mathematicians attempted a new tactic, the method of contradiction. If you want to prove something is true, you can pretend it is false, and use its falseness to prove as true something that definitely is false. That implies that your pretense was wrong, so the original thing must have been true.

So, let’s suppose the parallel postulate is false. Then either there is no line parallel to the given one, or else there’s more than one. Then something should go very wrong, and you’d know the parallel postulate was right.

But nothing goes wrong. You can do geometry perfectly well in either of these ways. Everything works fine. So these several mathematicians had accidentally discovered “non-Euclidean geometry.” Its horrific significance remained obscure for several decades, but by the late 1800s, a toxic unease seeped out into the culture. What if—surely not, it would not be possible—but what if it were not just a trivial oddity—what if it were not just a theoretical possibility with no relevance to reality—what if it were true?

Fyodor Dostoevsky’s 1880 novel The Brothers Karamazov was a foundational text for both nihilism and existentialism. It concerns problems of faith, free will, reason, and morality, driven by then-new conflicts between religion and rationalism, represented by two brothers with sharply differing views. In the philosophically central chapter, the rationalist brother invokes non-Euclidean geometry as an example of something that, like God’s creation, may be true but cannot be accepted by a rational mind:

If God exists and if He really did create the world, then, as we all know, He created it according to the geometry of Euclid and the human mind with the conception of only three dimensions in space. Yet there have been and still are geometricians and philosophers, and even some of the most distinguished, who doubt whether the whole universe, or to speak more widely, the whole of being, was only created in Euclid’s geometry; they even dare to dream that two parallel lines, which according to Euclid can never meet on earth, may meet somewhere in infinity. I have come to the conclusion that, since I can’t understand even that, I can’t expect to understand about God.

Space and time are bent. What??

After the “end of physics,” all that was left was more precise measurement. Unfortunately, one of those measurements went terribly wrong. It blew up physics, blew up rational certainty, blew up modernity, and nearly literally blew up the whole world with nuclear weapons in the Cold War.

It was the Michelson-Morley experiment of 1887, which measured the speed of light with unprecedented precision. Light is a wave, like waves on a pond. If you throw a rock in from a moving boat, the waves travel away faster behind than in front, because the boat is moving relative to the water. The earth is traveling through space, so light should likewise appear to travel away faster behind than in front. Michelson and Morley found it doesn’t. It travels at the same speed in all directions.

That answer couldn’t be right. It contradicted fundamental principles of physics, not to mention rationality and common sense. However, it was right, as several scientists found when they repeated the experiment.

Einstein’s theory of relativity solved that problem, but only at a hideous cost.

Relativity is based on non-Euclidean geometry. Space itself is warped, so the parallel postulate is not true. In physical reality, parallel lines can meet. It was bad enough when Euclidean geometry turned out to have alternatives in the abstract. Discovering that this one thing every educated person was most certain of was actually false was horrifying. What else might turn out to be wrong?

Well, Newton’s theory of gravity, more certain than God, was also false. Einstein published the theory of general relativity in 1915, but the catastrophe came to public consciousness only in 1919, with the Eddington experiment which showed that the sun’s mass bends space, so light from distant stars appears to be deflected as it passes by.

Massive opposition from both intellectuals and the general public followed. There were anti-relativity organizations, anti-relativity conventions, organized anti-relativity letter-writing campaigns, and books and articles and newspaper editorials denouncing it. It couldn’t be true, because it mustn’t be true, so it was false and wicked.

Who cares about gravity? No one. That wasn’t the point.¹⁰

The shock was to ethics, politics, aesthetics: systems of meaning. The systematic mode had justified them on the unshakable foundation of rationalism. Minor cracks had appeared already in the late 1800s. Those were plastered over, but Euclid and Newton were the prime certainties. Their fall has undermined rationalist confidence ever since. If those were wrong, anything or everything else might also come crashing down. The moral authority of science never fully recovered.

The public understood the Eddington experiment news as:

SCIENTISTS PROVE: NOTHING MAKES SENSE
Anything You Believe May Be Wrong.
No Absolute Truths, Authorities Insist
Everything shall be merely relative henceforth.

That would have made no sense before World War I, but it did make sense in 1919. It was a powerful confirmation of everyday experience during the war and in the chaotic postwar world. Amidst the pervasive feeling that something essential had broken down, many seized on relativity as a symbol of the general disintegration of meaning at the time.

Cultural theorists of the era described an epochal shift in the way people understood meaning in general. This is difficult to empathize with now, due to subsequent wholesale re-thinkings of meaningness, and of the nature of scientific knowledge.

Relativity doesn’t undercut rationality as such; it’s just a more complicated physical theory. It fails as a potential replacement for Newtonian physics as a prototype for absolutist systems of meaning. Relativity lacks key resources for that:

• It extensively violates common sense. Time runs slower near big things; the same events can occur in different orders for different objective observers; just going faster makes you heavier and shorter—without any limit, as you approach the speed of light. Meaning shouldn’t misbehave like that.

• Hardly anyone can understand relativity, so most people couldn’t understand social or cultural systems modeled on it, and couldn’t live within them.

• Relativity is complicated and mathematically difficult. Why would God have created an incomprehensible universe when He could have made a nice simple Newtonian one that would have worked just as well? If He did, why would we take that bizarre contraption as a model for meaning?

The popular influence of relativity mainly came from misunderstanding it as “relativism”: a recognition of nebulosity, more or less.

The theory of Einstein is a marvelous proof of the harmonious multiplicity of all possible points of view. If the idea is extended to morals and aesthetics, we shall come to experience history and life in a new way.
—Philosopher José Ortega y Gasset, 1923

• Relativity, or –ism, seemed consonant with the new celebration of incoherence in aesthetics. Some theorists hailed relativistic spacetime distortion as inspiration for Cubist and Futurist painting, for instance.¹¹ Others condemned relativity for the same reason.

• Many opponents, and some advocates, misunderstood it as moral relativism.

• Much opposition came from political conservatives, who saw it as a challenge to the established order.

• Some on the left said that nothing should be true unless everyone could understand it, so relativity was elitist and anti-democratic and must be stopped.

Many misunderstood relativity as a revelation of nebulosity, and therefore a disproof of rationalism. It was not; it is an absolute, deterministic system, formally similar to Newtonian mechanics.

More sophisticated thinkers understood relativity’s true challenges to rationalism:

• Certainty in the Euclidean, Newtonian worldview had been misplaced. How did that happen? How could we make sure never to make a mistake like that again? Science was believed to deliver absolute truth, but had gone wrong; what needed to change?

• Rationalism had used the eternalist certainty of Newtonian physics as its model for systems of meaning. What other conceptual system of certainty could justify ethics, politics, or aesthetics?

During the 1920s, scientists and philosophers felt they were making significant progress on these problems. Mathematical logic, they thought, could deliver absolute certainty, and science should be re-founded on that. The “Vienna Circle” of extraordinary scientists, mathematicians, and philosophers played a central role: in making sense of relativity, in the logical positivist program of proving the scientific method correct, and in grounding politics and ethics in science and rationality.

Then quantum hit, making the defense of rationalism still harder.

Quantum, worser than relative

Quantum theory is worse than relativity in three ways.

• Where Einstein’s mathematics was difficult but elegant, quantum theory is insanely complicated and just ugly. It’s a glued-up assemblage of too many ill-fitting bits with jagged edges and spikes that extend to infinity.¹² It’s impossible to imagine how the ultimate nature of reality could be such a rat’s nest.

• Quantum reveals that reality is inherently random and inherently unknowable. This seemed fatal for rationalism’s promises of ultimate certainty and control. Precise prediction of individual events is absolutely impossible. That is not due to human limitations, but intrinsic to the fundamental nature of the physical universe. Unlike relativity, quantum actually does reveal an aspect of nebulosity.¹³

• Whereas it takes several years of university math and physics to understand relativity, no one can understand quantum theory.¹⁴ Quantum violates common sense even more than relativity. The wave-particle duality and wave function collapse created major metaphysical difficulties for the first quantum physicists, and remain completely baffling.

Experimental tests of quantum theory make it the most precisely accurate and certain in all of science. It’s a triumph for technical rationality, meaning “the application of mathematics to the material world.” It was a severe challenge to rationalism, “the belief that correct thinking can yield perfect certainty, understanding, and control.”

The same Vienna Circle of physicists and philosophers who tried to revise rationalism to accommodate relativity’s paradoxes also took on the quantum paradoxes when they arrived a decade later. They did not succeed.

Mathematics is built on clouds

Meanwhile, mathematics was having its own foundational crisis. It turned out that, like quantum physics, mathematics itself puts intrinsic, absolute limits on certainty, knowledge, and understanding. That wrecked the project of re-founding science on mathematical logic, and eventually all hope of finding anything we can be certain of.

Trouble began in the 1870s, with Georg Cantor’s discovery that there are different sizes of infinities. That created major problems for meaning, because philosophers and theologians had held for thousands of years that God was the only “actual infinity.” The numbers 1, 2, 3, … were only “potentially infinite”: you could keep on going, but you’d never get to infinity, because God is transcendent. Cantor went there. He went beyond there, and discovered more bigger infinities. He proved that there can be no biggest infinity. Oh no! How big is God, then?

Many prominent mathematicians denounced Cantor as a “scientific charlatan”, “renegade,” and “corrupter of youth,” and demanded that his work be banished from mathematics as anti-rational. Cantor himself believed that his discoveries disproved both materialism and determinism.¹⁵

Another crisis for rationalism: mathematical proof was supposed to compel agreement, establishing certainty beyond any possibility of doubt. Mathematics was meant to be absolute truth, not a mere matter of opinion. Yet the leading mathematicians of the era held sharply disagreeing opinions about actual infinities, and whether proofs of them were valid. There seemed to be no way to resolve the dispute.

Further, the mathematics generated a series of paradoxes. If you did accept actual infinities, you were led to logical contradictions. The best known is Russell’s paradox: does the infinite set of all sets that do not contain themselves contain itself? (If it does not contain itself, then it must, but if it does contain itself, it mustn’t.)

Since the mid-twentieth century, most mathematicians have accepted Cantor’s actual infinities as existent and important.¹⁶ In fact, his work is now the basis for all the rest of mathematics. It turned out that most ordinary, finite numbers are actually hard shells that encapsulate an actual infinity crammed inside under enormous pressure.¹⁷ If you delete the actual infinities from mathematics, what’s left is ugly wreckage, and not much of it. In particular, calculus mostly doesn’t work, and if you can’t do calculus, you can’t do physics.

This cast the whole enterprise of mathematics into question. It can’t be done without actual infinities, but allowing actual infinities apparently led to metaphysical monsters and outright logical contradictions. Might the whole edifice topple as its foundations crumbled? Might mathematics devolve into pure aesthetic opinion, like postmodern film criticism?

David Hilbert, who had made major contributions to the mathematics of both relativity and quantum, led the way forward. “No one shall expel us from the Paradise that Cantor has created.” The solution, he proposed, would be a more rigorously rational approach to mathematical proof, which should eliminate all room for error and opinion. He aimed then to prove that all mathematical truths could be proven: that mathematics is complete, so that everything can be demonstrated to be either true or false using objective rationality. This would also eliminate all internal contradictions, such as Russell’s paradox. Then at last rationality could deliver the absolute certainty the Ancient Greeks fantasized about, and which it had seemed Newton had discovered—but now without any possibility of further unwelcome surprises.

Then, many philosophers believed, the correct political, economic, ethical, and psychological systems could be proven correct, beyond all possibility of doubt. Here the intellectual world of just a century ago seems as alien to me as the religion of the Sumerians. How could the smartest people of that era imagine such a thing was possible? The Vienna Circle, among others, put great effort into it. Success would eliminate much conflict and suffering, and we wouldn’t have to have wars or depressions or waves of immorality and irrationality ever again.

A drastically unwelcome surprise arrived in 1931. Kurt Gödel proved that not all mathematical truths can be proven, by any means whatsoever. It is also impossible to prove that mathematics is free of internal contradictions. This showed that rationality is incomplete and certainty is permanently out of reach—as the quantum uncertainty principle had also shown, but now at an even more fundamental level.¹⁸

You read essays by Hermann Weyl or John von Neumann [prominent physicist-mathematicians of the era] saying things like this: I became a mathematician because this was my religion, I believed in absolute truth, here was beauty, the real world was awful, but I took refuge in number theory. And all of a sudden Gödel comes and ruins everything, and I want to kill myself!¹⁹

Once again, it fell to the long-suffering Vienna Circle to try to patch up rationalism to accommodate the blow. Dispersed by the Nazis, they kept at it in exile into the 1950s, but the cause was hopeless. Rationalism had conclusively, irreparably, permanently failed.

Science and mathematics after certainty

Karl Popper was the first to admit that science cannot ever, even in principle, justify certainty.²⁰ Science proceeds, he said, by replacing old theories with better ones, as when relativity replaced Newtonian gravitation and quantum replaced Maxwell’s electromagnetic theory. However, the new ones must be assumed to be somewhat false as well.

A vague descendent of Popper’s theory replacement framework provided a new triumphant narrative for public explanations of scientific progress, which deliberately obscures the foundational crisis and rationalism’s failure:

Relativity and quantum were huge successes! They prove that science works. They are better than the physics of the 1800s! And even though we know they must still be slightly wrong, inevitably we’ll find a super-theory that combines both, corrects their errors, and explains everything.

Scientific progress is a fact, and understanding how and why it happens would be tremendously valuable. However, having dispelled the rationalist hope that a criterion of conclusive evidence could prove a theory correct, Popper did not explain what makes a scientific theory “better,” or where new ones come from.

Thomas Kuhn’s 1962 The Structure of Scientific Revolutions showed that there are no fixed criteria. “Better” theories are often less good at predicting experimental results initially. Major scientific advances are social processes during which a community gradually changes allegiance to a new way of thinking, typically based on multiple nebulous considerations. That process is not rational, although it is also not irrational—it is meta-rational.

The “paradigm shift” produces an “incommensurable” ontology: a new way of seeing the world, not just a different theory of the same thing. Newton’s theory of gravity describes an attractive force between objects. Einstein’s theory of gravity does not involve any force; it describes the shape of spacetime.

Anti-rationalism in the countercultures

The next chapter discusses the two countercultures of the 1960s–90s: the hippie/New Age movement and the Evangelical Christian movement. Both justified their explicit rejections of rationality in terms of the failure of rationalism in the wake of the foundational crises.

One thread of irrationalism insists that “my truth” is just as valid as “your” truth because there is no fixed criterion. This was typical of the hippie counterculture. “Don’t you know Einstein proved it’s all relative, man?” was a common response to any rational criticism.

Kuhn’s work was misunderstood as a general justification for relativism and for replacement of rationality with way-out speculation. Square Establishment ideas about what is possible and proper were the outmoded old paradigm. Whatever revolutionary fantasies about politics, ethics, or cosmic metaphysics you found attractive were the new paradigm, which should and would replace it. The supposed relativism of The Structure of Scientific Revolutions also influenced nihilistic postmodernism’s attack on systematicity.²¹

Both the quantum uncertainty principle and Gödel’s work were misunderstood as validations of everyday uncertainty, which has entirely different sources. “Even in mathematics, that supreme bastion of reason, truth is either beyond us or a matter of more or less arbitrary consensus rather than objective fact.”²² Fortunately, since science no longer makes any sense, it has no relevance for the everyday world. No matter what your opponents say about society and culture, there’s no way they could prove they are correct! Therefore, your wacky opinions are unassailable.

A supposed obscure connection between consciousness and quantum phenomena justified any sort of New Age monist mystical flummery. Gödel’s proof of the limits of formal systems justified the superiority of creative human insight over sterile mechanical rationality. See, our intuitive belief in healing crystals is proven by the new-paradigm science!

The Evangelical counterculture attempted to restore Christianity as an absolute foundation for systems. The nineteenth century synthesis of Christianity and rationalism had weakened the religion so much that by the 1970s it seemed on its way out. Evangelical anti-rationalism tried to reverse that, restoring Biblical literal inerrancy as a basis for morality and social order. Leaders of the movement pointed out that rationalism had discredited itself. Some alluded to Gödel as proof that “since mathematics cannot prove its own consistency, reason is powerless to justify itself, so that either there is no justification to be had, or reason can be supported only by faith.”²³

The loss of elite confidence

The main legacy of the foundational crises was loss of social confidence, rather than practical technical problems.

The systematic mode was imposed by elites on a populace that never wanted it (although they massively benefited from it on average). The elites’ power and willingness to exercise it depended on their unquestioning confidence in their rational and religious justifications, and therefore in their own social, cultural, and moral authority. By the 1960s, they understood—better than the populaces they commanded—that their justifications had failed, and their systems were built on clouds.

When the countercultures challenged the elite establishment, it caved almost immediately. It was hollow, running only on momentum. The ruling class knew they had no justification for their authority apart from preexisting power, which (to their credit) they were unwilling to fully exercise. It’s not that they thought “Well, Gödel’s Incompleteness Theorem says I don’t really know anything, so probably the hippies and queers and addicts are right.” It’s that they weren’t taught that Euclid shows rationality provides certainty. For Victorian elites, it was inconceivable that sane people could contest the Law And Order agenda. In 1970s America, everything could be doubted, at least in principle… so, however misguided, maybe the kids had a point about the war at least.

Having lost their self-confidence, when anti-rationalist barbarians battered the gates, the establishment hemmed and hawed for a few years, and then just turned over the keys.

Reclaiming rationality in the fluid mode

Rationality is better than irrationality. It can be massively valuable when it works. There is never a guarantee that it will, but it often does. Science often works, and drives much of material progress. Rationality is an important tool for evaluating claims in dimensions of meaning such as ethics, politics, and aesthetics as well.

Absolute certainty is impossible, but effective certainty is common. No method of reasoning can be guaranteed correct, but many technical methods are quite reliable within particular domains.

Throughout the twentieth century, investigation of how rationality and science work concentrated on the traumatic events of the foundational crises. Those are atypical, nearly unique examples, and therefore a bad basis for a broader understanding. Theories that sought to explain them fail to describe most other scientific and technical work.

The theoretical problems discovered during the foundational crisis are dissimilar to the difficulties faced in real-world technical work. When rationality and science fail in practice, as they often do, it is almost never due to quantum uncertainty or Gödel issues. And, when they succeed in practice, the reasons are quite different from the mistaken theories promoted by rationalism.

After rationalism got falsified, we collectively failed to replace that old paradigm with a better understanding of how and why rationality works. That enabled the anti-rational countercultures, nihilistic postmodernism, and contemporary atomized know-nothing populism to discredit and ignore it. All our systems, social and cultural and psychological as well as technical, are falling apart as a consequence.

A shift into the fluid mode to create new functional systems will require recovering respect for rationality on a new basis. My book In the Cells of the Eggplant sketches how.